Modelling the Slitherlink Problem
In the Slitherlink problem, we are given an \(n \times m\) grid. A cell in the grid can be empty or contain a number between 0 and 3. Each cell has 4 associated edges (its borders). The goal is to select a set of edges among all cells such that:
If a cell has a number \(k\), then \(k\) of its edges have to be selected.
The selected edges form exactly one cycle that does not cross itself.
 Slitherlink input example
|
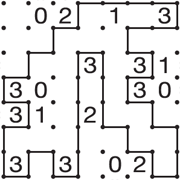 Solution example
|
In this figure we can see an example of the Slitherlink problem and its only correct solution.
To model and solve the Slitherlink problem we will use the following Python class (we will add more methods later when we need them):
1class SlitherLink:
2 def __init__(self, path):
3 with open(path) as f:
4 self.cells = [
5 [None if char in ["-", "."] else int(char) for char in line.strip()]
6 for line in f
7 ]
8 self.n = len(self.cells)
9 self.m = len(self.cells[0])
10
11 def edge(self, i, j, dir):
12 # We represent each edge using a boolean variable where:
13 # - (i, j) is the position of its "top-left" vertex of the edge
14 # - "dir" is the direction of the edge
15 return Bool(f"Edge_{i}_{j}_{dir}")
16
17 def vertex_edges(self, i, j):
18 intersection = []
19 if i > 0:
20 intersection += [self.edge(i - 1, j, "right")]
21 if j > 0:
22 intersection += [self.edge(i, j - 1, "down")]
23 if i < self.m:
24 intersection += [self.edge(i, j, "right")]
25 if j < self.n:
26 intersection += [self.edge(i, j, "down")]
27 return intersection
28
29 def cell_edges(self, i, j):
30 return [
31 self.edge(a, b, dir)
32 for a, b, dir in [
33 (i, j, "right"),
34 (i, j, "down"),
35 (i + 1, j, "down"),
36 (i, j + 1, "right"),
37 ]
38 ]
The following code snippet shows the source code needed to model into SAT an instance of the problem. First, we generate an instance of the class Problem (line 3). Then, we encode the constraints of the problem. Lines 5-12 encode the vertex constraints that ensure that the path traced by the solution is contiguous. Line 8 calls the method vertex_edges, that returns a list of Bool objects representing edges that intersect at the vertex i,j. Lines 9-12 encode the constraint for the edges of a vertex. A selected edge can be contiguous without crossing iff the number of selected edges that intersect at each vertex is 0 or 2.
Lines 15-19 encode the cell constraint for each cell with a number. Line 18 calls the method cell_edges, which returns a list of Bool objects representing the edges that surround a cell. Line 19 adds the constraint to the Problem instance.
Then, we encode the problem to CNF DIMACS (line 21) applying the Tseitin transformation [Tse83] and return the underlying CNF object.
1def encode_slitherlink(sl):
2
3 p = Problem()
4
5 # Vertex Constraints
6 for i in range(sl.m + 1):
7 for j in range(sl.n + 1):
8 edges = sl.vertex_edges(i, j)
9 p.add_constr((Add(edges) == 0) | (Add(edges) == 2))
10
11 # Cell Constraints
12 for j, row in enumerate(sl.cells):
13 for i, cell in enumerate(row):
14 if cell is None:
15 continue
16 edges = sl.cell_edges(i, j)
17 p.add_constr(Add(edges) == cell)
18
19 return p.to_cnf_dimacs()
Notice that this model is not taking into account the fact that there has to be exactly one cycle.